长篇解读扩散模型 | Stable Diffusion

前言

本文将解读目前最受欢迎的人工智能图像生成模型之一，稳定扩散模型（Stable Diffusion Models, SD）^[1]，该模型能够通过简单的文本描述生成出非常真实的描述图像。

先前的扩散模型（Diffusion Model, DM）是将图像形成过程分解为去噪自编码器的连续应用（编码器-解码器）， 并且允许一种指导机制来控制图像生成过程，而无需重新训练。但是需要大量的时间和GPU，推理成本高昂

为了提高这类模型的可用性，同时减少其对资源的大量消耗，需要一种方法来降低训练和采样的计算复杂度。

该文^[1:1]提出了一种全新的潜在扩散模型（latent diffusion models, LDMs)），为了在有限的计算资源上进行训练，同时保持其质量和灵活性，采用了几个方法：

1. 在预训练的自动编码器的隐空间中应用了扩散模型； 采用这种方法训练扩散模型，首次在降低复杂性和保留细节之间达到近乎最佳的平衡点，从而大大提高视觉保真度。
2. 在模型架构中引入交叉注意层，将扩散模型转化为强大而灵活的生成器。 可用于文本或边界框等一般条件输入，并以卷积方式实现高分辨率图片合成。

该模型在文本到图像合成、无条件图像生成和超分辨率等领域达到了SOTA层次（截止2022年），并显著降低了计算要求。

研究思路

大众化的高分辨率图像合成

扩散模型在计算上仍然要求很高，因为训练和评估这样的模型需要在RGB图像的高维空间中重复进行评估和梯度计算，这将消耗大量时间和存储空间。

为了提高这类强大模型的可用性，同时减少其对资源的大量消耗，需要一种方法来降低训练和采样的计算复杂度。

原先的扩散模型训练需要多少时间？

举例来说，训练最强大的扩散模型通常需要数百个 GPU 日（一张V100需要150~1000日^[2]）

在输入空间的高噪声版本上重复评估也使推理变得昂贵，在一张 A100 GPU 上生成 50k 个样本大约需要 5 天 ^[2:1]。

这给研究界和广大用户带来了两个后果：

• 首先，训练这样一个模型需要大量的计算资源，而这些资源只有该领域的一小部分人才能使用，并且会留下巨大的碳足迹（不够环保）。
• 其次，评估已训练好的模型在时间和内存上也很昂贵，因为同一模型架构必须连续运行大量步骤^[2:2]。

从潜在空间出发

原文图2：感知压缩和语义压缩

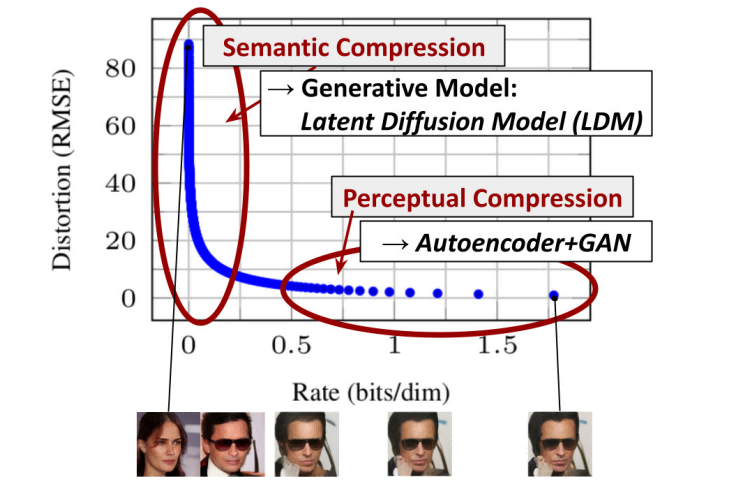
文章分析了已训练好的扩散模型，如上图所示，模型的学习过程可以大致分为两个阶段：

1. 感知压缩阶段：其删除原图的许多高频细节，学习到的语义变化很少
2. 语义压缩阶段：对数据的语义和概念组成（语义压缩）进行学习

从我的理解上就是编码、解码的过程

文章的做法是，将训练分为两个不同的阶段：

1. 首先训练一个自编码器，其提供一个低维的表示空间，感知上相当于数据空间。

   与之前的工作相比，不需要依赖过度的空间压缩，因为在学习到的隐空间中训练扩散模型在空间维度方面表现出更好的缩放特性， 降低的复杂性还可以通过单次网络传递从隐空间高效生成图像。因此文章将生成的模型类称为“隐式扩散模型”。

   这种方法的一个显著优点是，在通用自编码阶段我们只需要训练一次，因此可以将其重复用于多个扩散模型的训练，或探索可能完全不同的任务。

   这使得能够有效地探索各种图像到图像和文本到图像任务的多种扩散模型

2. 将Transformer连接到扩散模型的UNet的骨干网络，并启用任意类型的基于token的条件机制。

提出的方法

为了降低训练扩散模型对高分辨率图像合成的计算需求（需要更多设备）， 我们观察到尽管扩散模型允许通过欠采样相应的损失项来忽略感知上不相关的细节， 但它们仍然需要在像素空间中进行昂贵的函数评估，这导致了巨大的计算时间和能源需求。

什么是欠采样相应的损失项？

即不是在每个像素上计算损失，而是选择图像的一个子集（例如，通过降低分辨率或随机选择像素）来计算损失

作者提出了一个建议，即通过引入压缩阶段与生成学习阶段的明确分离，来解决现有方法中存在的问题。

为了实施这一建议，他们采用了一个自动编码模型。 这个模型的特点在于，它能够学习一个与图像空间在感知上等同的空间，但计算复杂性却显著降低。

换句话说，该模型能够在保留图像主要特征的同时，减少处理这些图像所需的计算资源。

接着，作者列举了这种方法所具有的几个优点：

1. 通过离开高维图像空间，即在较低维度的空间上进行采样，可以显著提高计算效率。 这是因为高维数据通常需要更多的计算资源来处理，而通过将数据映射到低维空间，可以在保留关键信息的同时，减少不必要的计算开销。

2. 该方法利用了从其UNet架构中继承的归纳偏差，这使得模型在处理具有空间结构的数据时特别有效。

什么是归纳偏差？

归纳偏差在训练算法时采用的一些先验性假设（根据一些经验）或限制，以帮助模型更好地泛化和学习数据的特征， 这有助于减轻对以前方法所要求的积极的、降低质量的压缩级别的需求。

换句话说，由于模型能够更好地理解和处理空间结构数据，因此不需要像以前那样进行大幅度的压缩来降低数据质量。

3. 通过这种方法获得的压缩模型具有通用性。 其潜在空间不仅可以用于训练多个生成模型，还可以应用于其他下游任务（如单幅图像clip引导合成）。 这意味着该压缩模型不仅适用于特定的应用场景，还可以作为一种通用的工具，为各种图像处理任务提供支持。

感知图像压缩（Perceptual Image Compression）

作者提出的感知压缩模型基于前人工作，并由两部分组成：

1. 感知损失
2. 基于 Patch 的对抗目标相结合训练的自编码器。

这确保了通过加强局部真实性来确保重建限制在图像流形内， 并避免了仅依赖像素空间损失（例如 $L_2$ 或 $L_1$ 目标损失）而引入的模糊。

更准确地说，给定 RGB 空间中的图像 $x\in {\mathbb{R}}^{H\times W\times 3}$ ， 编码器 $\mathcal{E}$ 将 $x$ 编码为隐式表示 $z=\mathcal{E}(x)$ ， 解码器 $\mathcal{D}$ 从隐图像中重建图像，得到 $\tilde{x}=\mathcal{D}(z)=\mathcal{D}(\mathcal{E}(z))$ ， 其中 $z\in {\mathbb{R}}^{h\times w\times c}$ 。重要的是，编码器按比例 $f=H/h=W/w$ 对图像进行下采样， 并研究了不同的下采样因子 $f=2^m$ ，其中 $m\in \mathbb{N}$ 。

为了避免任意高方差的隐空间，作者尝试了两种不同类型的正则化：

1. KL-reg：对学习到的隐变量施加一个小的KL惩罚，使其接近标准正态分布，类似于变分自编码器（VAE）；
2. VQ-reg：在解码器中使用矢量量化层，类似于VQ-GAN，但是量化层被解码器吸收。

这为使得 扩散模型 与 学习到的隐空间 $z=\mathcal{E}(x)$ 的二维结构一起工作，可以使用相对温和的压缩率，并实现非常好的重建，更好地保留了 $x$ 的细节。

隐式扩散模型

扩散模型是一种概率模型，旨在通过逐渐对正态分布变量进行去噪来学习数据分布 $p(x)$， 这对应于学习长度为 $T$ 的固定马尔可夫链的逆过程。

对于图像合成，最成功的模型依赖于 $p(x)$ 上的变分下界进行重新加权的变体，其反映了去噪分数匹配。

这些模型可以解释为去噪自编码器 ${ϵ}_{\theta }(x_t,t);t=1...T$ 的等权重序列， 其被训练于预测输入 $x_t$ 的去噪变体，其中 $x_t$ 是输入 $x$ 的噪声版本，$t$ 从 $\{1,...,T\}$ 中均匀采样。相应的目标可以简化为（详细推理见原文附录B）：

$$\begin{array}{}\text{(1)}& L_{DM}={\mathbb{E}}_{x,ϵ\sim \mathcal{N}(0,1),t}\left[{\Vert ϵ-{ϵ}_{\theta }(x_t,t)\Vert }_2^2\right]\end{array}$$

公式一览

• ${\mathbb{E}}_{x,ϵ\sim \mathcal{N}(0,1),t}$： 表示对数据输入 $x$、 从标准正态分布 $N(0,1)$ 中采样的随机噪声 $ϵ$，以及时间变量 $t$ 来计算相应的期望。
• $\left[{\Vert ϵ-{ϵ}_{\theta }(x_t,t)\Vert }_2^2\right]$： 期望运算符作用的具体表达式，计算真实噪声与模型预测的噪声之间的欧几里得距离的平方
  • $ϵ$：生成的随机噪声
  • ${ϵ}_{\theta }(x_t,t)$：去噪模型去除的噪声

什么是变分下界？

变分下界是变分推断中的一种技术，用于评估近似概率分布的质量。

它的核心思想是找到一个近似概率分布 $q(x)$ 来逼近真实的概率分布 $p(x)$。 变分下界通常用于求解最优的近似分布，其计算涉及到对概率分布的积分或期望的估计

隐式表示的生成建模（Latent Diffusion Models）

通过训练好的由 $\mathcal{E}$ 和 $\mathcal{D}$ 组成的感知压缩模型， 可以访问一个高效、低维的隐空间，其中高频、不可察觉的细节被抽象了出来。

与高维像素空间相比，该空间更适合基于似然的生成模型，有两个优点：

1. 专注于数据的重要语义部分
2. 在较低维度的空间进行训练，计算更高效

之前的研究依赖于在高度压缩的离散隐空间之中，采用自回归的、基于注意力的 Transformer 模型，与之不同的是， 我们可以利用模型提供的、特定于图像的归纳偏置。 这包括主要从 2D 卷积层构建底层 UNet 的能力， 并使用重新加权的边界进一步将目标集中在感知最相关的部分上，现在为

$$\begin{array}{}\text{(2)}& L_{LDM}:={\mathbb{E}}_{\mathcal{E}(x),ϵ\sim \mathcal{N}(0,1),t}\left[{\Vert ϵ-{ϵ}_{\theta }(z_t,t)\Vert }_2^2\right]\end{array}$$

提出模型的骨干网络 ${ϵ}_{\theta }(\circ ,t)$ 被实现为时间条件的UNet。 由于前向过程是固定的，因此可以在训练其间从 $\mathcal{E}$ 高效获取 $z_t$ ， 可以通过 $\mathcal{D}$ 一次性将来自 $p(z)$ 的样本解码到图像空间。

公式变化分析

新的 $L_{LDM}$ 模型损失公式 与原先 $L_{DM}$ 区别在于：

1. 将原先的输入图像 $x$ 编码为 $z=\mathcal{E}(x)$
2. 编码后的数据 $z$ 会根据时间变量 $t$ 和随机噪声 $ϵ$ 构造 新的噪声数据 $z_t$

简单说就是，将从原先的图像空间转移到现在的隐空间上，后续通过 $\mathcal{D}$ 还原至原图像空间

条件机制（Conditioning Mechanisms）

与其他类型的生成模型类似，原则上扩散模型能够对 $p(z|y)$ 形式的条件分布进行建模。

条件概率

$p(z|y)$ 指的是在给定 $y$ 已经发生的条件下，随机变量 $z$ 的概率分布。

这可以通过条件去噪自编码器 ${ϵ}_{\theta }(z_t,t,y)$ 来实现， 并为通过输入 $y$ （例如文本、语义图或其他图像到图像的翻译任务）来控制合成过程铺平了道路。

然而，在图像合成的背景下，将 DM 的生成能力与类标签或输入图像的模糊变体之外的其他类型的条件相结合， 迄今为止是一个尚未充分探索的研究方向。

我们通过交叉注意力机制增强其底层 UNet 的骨干网络，将 DM 转变为更灵活的条件图像生成器， 这对于学习各种输入模态的基于注意力的模型非常有效。

为了预处理来自各种模式（例如：语言 prompts）的 $y$， 我们引入了一个特定域编码器 ${\tau }_{\theta }$ ， 它将 $y$ 投影到中间表示 ${\tau }_{\theta }(y)\in {\mathbb{R}}^{M\times d_{\tau }}$ ， 然后通过交叉注意力层映射到 UNet 的中间层，如下:

$$\begin{array}{r}\text{Attention}(Q,K,V)=\text{softmax}\left(\frac{Q{K}^T}{\sqrt{d}}\right)\cdot V\end{array}$$

其中 $Q=W_Q^{(i)}\cdot {\phi }_i(z_t),K=W_K^{(i)}\cdot {\tau }_{\theta }(y),V=W_V^{(i)}\cdot {\tau }_{\theta }(y)$ 。

注意

• $W_V^{(i)}\in {\mathbb{R}}^{d\times d_{ϵ}^i},W_Q^{(i)}\in {\mathbb{R}}^{d\times d_{\tau }},W_K^{(i)}\in {\mathbb{R}}^{d\times d_{\tau }}$ 是可学习的投影矩阵。
• ${\phi }_i(z_t)\in {\mathbb{R}}^{N\times d_{ϵ}^i}$ 是 UNet 实现 ${ϵ}_{\theta }$ 的（扁平化）中间表示

公式部分解读

$Q,K,V$ 的处理进行分解：

• $Q=W_Q^{(i)}\cdot {\phi }_i(z_t)$：噪声输入 $z_t$ 经过去噪编码器 ${ϵ}_{\theta }$后的第 $i$ 层的中间表示，乘上 第$i$层的可学习的矩阵 $W_Q^{(i)}$ 后，得到 $Query$
• $K=W_K^{(i)}\cdot {\tau }_{\theta }(y)$：某种模式的输入 $y$（例如：语言prompt） 通过特定域编码器 ${\tau }_{\theta }$ 映射到中间表示 ${\tau }_{\theta }(y)$， 乘上第 $i$ 层的可学习的矩阵 $W_K^{(i)}$， 得到 $Key$
• $V=W_V^{(i)}$：$K$中相同的中间表示 ${\tau }_{\theta }(y)$， 再乘上第$i$层的可学习的矩阵 $W_V^{(i)}$，得到 $Value$

参见图 3 中的描述。

图3

图3注释版，图片出处

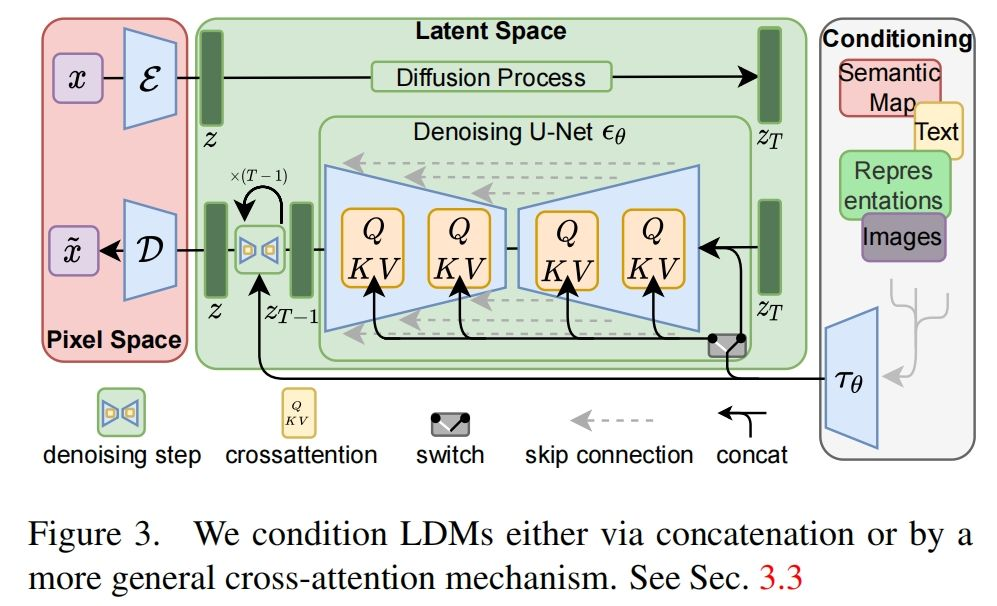
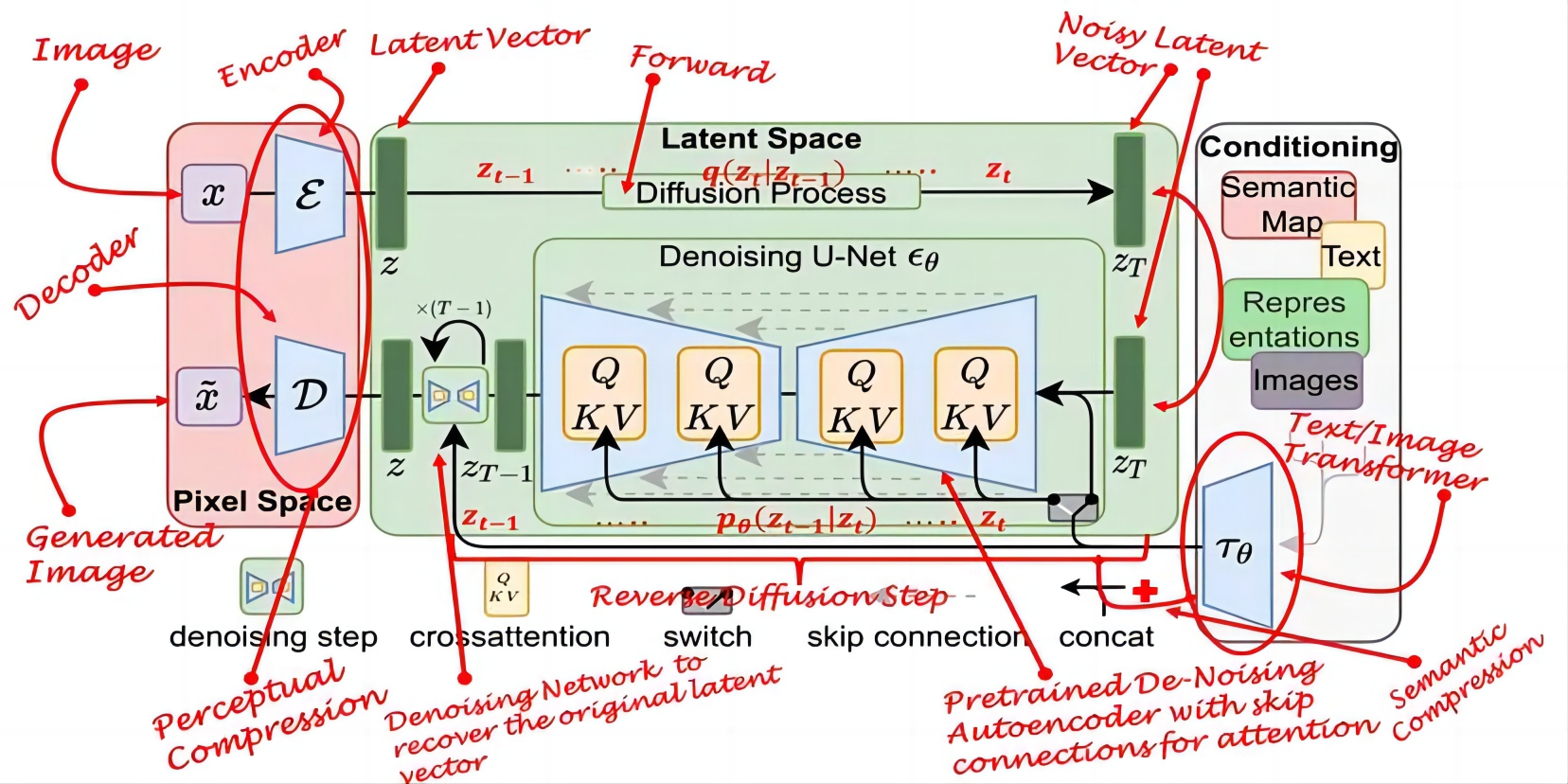
基于图像-条件对，我们随之通过以下方式学习条件 LDM，

$$\begin{array}{}\text{(3)}& \begin{array}{r}{L}_{LDM}:={\mathbb{E}}_{\mathcal{E}(x),y,ϵ\sim \mathcal{N}(0,1),t}[\Vert ϵ-{ϵ}_{\theta }(z_t,t,{\tau }_{\theta }(y)){\Vert }_2^2]\end{array}\end{array}$$

${\tau }_{\theta }$ 和 ${ϵ}_{\theta }$ 通过方程 3 联合优化。

这种条件机制很灵活，因为 ${\tau }_{\theta }$ 可以通过特定领域的专家进行参数化；例如当 $y$ 是文本 prompts 时可以是（无 mask 的）transformers 。

原文实验

后续补充

参考网络文章 & 论文来源

1. 使用隐式扩散模型进行高分辨率图像合成（SD原文直译）
2. Stable Diffusion 原理介绍与源码分析（一）
3. Stable Diffusion 原理介绍与源码分析（二、DDPM、DDIM、PLMS）

---

1. High-Resolution Image Synthesis with Latent Diffusion Models ↩︎ ↩︎

2. Diffusion Models Beat GANs on Image Synthesis ↩︎ ↩︎ ↩︎